Hoje venho falar de um problema bem interessante que achei no meio dos papéis aqui de casa. Estava numa apostila de cálculo 2, então resolvi tentar fazer:
Problema: Calcule a área contida entre a curva (polar) r = tan θ, o eixo horizontal e a reta (cartesiano) x = 1.
Minha Solução: Note que, como a distância à origem é
Então, temos um sistema de coordenadas paramétricas:
Agora, só precisamos calcular
Efetuando
Então
Logo,
Como o problema pede a área de 0 a 1, só temos que analisar a função para estes valores, e subtrair como numa integral definida. Como a expressão polinomial zera para ambos os valores, podemos apenas analisar
E essa é a área que desejamos.
Contudo, existe uma solução diferente, menos técnica que esta:
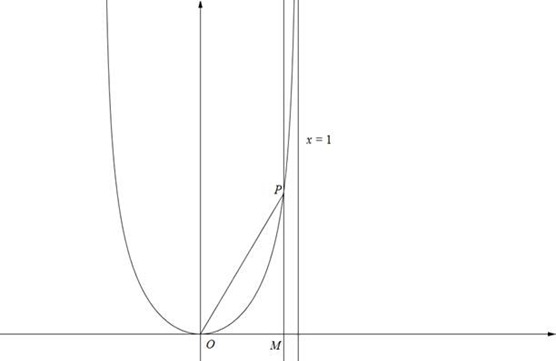
Solução do Livro: Seja, como na figura abaixo, o triângulo OPM:
A área que queremos é dada pela área do triângulo menos a área da função entre O e P. Esta área pode ser calculada através de uma integral em coordenadas polares. Porém, ao calcular a integral de 0 a π/2 diretamente a função, obtemos uma indeterminação. Como remediar isso? Através do nosso método, com o auxílio de um limite! Logo, Como
E a área da função é
De 0 a π/2. Agora, modificando a fórmula da área do triângulo:
Logo, nossa área total é
Vamos analisar, separadamente, o limite:
Agora, como o limite nos leva à indeterminação (0/0), podemos aplicar a regra de l’Hôpital, derivando tanto o denominador quanto o numerador da fração, para obter
Portanto, temos que o limite se anula, e, enfim
É interessante como um método técnico pode gerar uma solução trabalhosa, apesar de correta, enquanto um método mais livre requer muito mais raciocínio (claro, o truque de considerar o triângulo pode ser conhecido, mas para um leigo não vem tão facilmente), porém é capaz de fornecer soluções muito mais rapidamente, sem o recurso a repetidas integrais. Entretanto, ambos os métodos nos dão o resultado correto, o que destaca a importância de ambos.
Fiquem atentos ao blog para conteúdos novos sobre calculo diferencial.

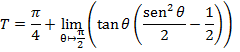
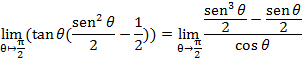
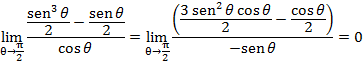
Olá,
ResponderExcluirachei o problema muito interessante, gostaria de saber de onde foi retirado(qual livro?).
Olá, Danfla!
ResponderExcluirNa verdade, como mencionei, era uma apostila qualquer de Cálculo 2. Não sei nem se ainda a tenho, muito provavelmente já a joguei fora. Mas, caso ache, volto a comentar aqui.
Abraço,
João Pedro Ramos.