Na continuação da nossa jornada pelo mundo dos espaços de Hilbert, analisemos mais um ponto de contato entre a teoria dos Espaços de Hilbert e a teoria de Espaços Vetoriais de Dimensão Finita. Esta conexão entre a Álgebra Linear e a Análise Funcional se dá, mais uma vez, por causa da similaridade entre a geometria nos dois casos. Isto se reflete no nosso próximo tópico, e o motivaremos com um exemplo: Se l²(N) é o espaço definido acima como das sequências quadrado-somáveis, então considere o conjunto dado por
Onde i varia pelos naturais. Se considerarmos o sentido usual de base, ou seja, um conjunto cujas combinações lineares finitas geram o espaço, então este conjunto claramente não é uma base: por exemplo, a sequência
Não está no span finito de tal conjunto, embora esteja em l²(N). Isto nos sugere que, embora queiramos que tal conjunto de sequências seja uma "base", em algum sentido, este não pode de jeito algum ser o sentido usual. Assim, devemos construir uma nova noção de base, onde tal conjunto de sequências possa se encaixar, e mesmo assim tenha propriedades interessantes que as bases de espaços de dimensão finita têm. Isto nos leva à seguinte
Definição: Seja H um espaço de Hilbert.
(1) Dizemos que uma sequência w = 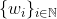 é uma base ortonormal para o espaço H se
é uma base ortonormal para o espaço H se
(i) 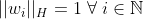
(ii) 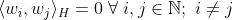
(iii) 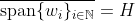 .
.
(2) Seja 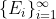 sequência de subespaços fechados de H. Dizemos que H é a soma de Hilbert
sequência de subespaços fechados de H. Dizemos que H é a soma de Hilbert
de tais espaços se
(i) Se i é diferente de j, então
(ii)
Ou seja, podemos dizer que uma sequência 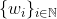 é uma base ortonormal se e só se
é uma base ortonormal se e só se
faz com que o espaço H seja a soma de Hilbert
É fácil, com essa definição, verificar que o subconjunto do espaço de sequências acima é uma base ortonormal. As bases ortonormais são objetos extremamente importantes da teoria de Espaços de Hilbert por nos proporcionarem, dentre outras coisas, maneiras simples de escrever elementos do nosso espaço, como nos diz o resultado abaixo.
Teorema 1: (Expansão de Fourier e Identidade de Bessel-Parseval).
Seja
Onde a projeção é aquela que definimos no tópico anterior, e os espaços E satisfazem a propriedade de soma de Hilbert.
Então as somas parciais
satisfazem que
E, ainda mais,
(Esta ultima igualdade sendo conhecida como a Identidade de Bessel-Parseval).
Se estivermos no caso de uma sequência w que é uma base ortonormal de H, então temos explicitamente que
Conhecida como Expansão de Fourier com relação à base ortonormal w.
Prova: Comecemos calculando
Por causa da ortogonalidade dos espaços considerados. Da definição, vemos que
Mas, da conta acima,
Portanto, parece razoável provar que 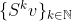 é de Cauchy, resultado expresso pelo próximo
é de Cauchy, resultado expresso pelo próximo
Lema: 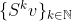 é Sequência de Cauchy, e converge para v em H.
é Sequência de Cauchy, e converge para v em H.
Prova: Vejamos que
Como sabemos que a série
E a parte na conta acima é justamente a cauda de tal série, que, como sabemos, tem de ir a zero, à medida que k,j crescem. Logo, garantimos que 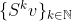 converge para um limite S.
converge para um limite S.
Agora, fixe u em 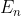 , e Note que, para k > n, então, pela propriedade da projeção,
, e Note que, para k > n, então, pela propriedade da projeção,
Fazendo 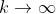 , é fácil obter que
, é fácil obter que
Usando tal Lema, é fácil concluir o teorema. 
Para ilustrar a utilidade de tal Teorema, vejamos um exemplo:
Exemplo 1: Considere o espaço das funções contínuas no intervalo [0,1]. Tome funções da forma exp{πikt}, com k em Z. Pelo Teorema de Stone-Weierstrass, sabemos que o span linear de tal conjunto de funções sobre C[0,1] é denso no subespaço das funções contínuas e periódicas CP[0,1]. Como esse último espaço é denso em L²[0,1] (ver exercícios), então temos que o conjunto de funções considerado é uma base ortonormal para L²[0,1], e temos que todo elemento u nesse último espaço se escreve como
Onde tal série é interpretada como L²-convergente, e
Chamamos de tal expansão também de expansão de Fourier de u.
Tal exemplo é crucial para a Teoria de Equações Diferenciais Parciais, e é uma das observações que motivaram mais ativamente o desenvolvimento da Análise de Fourier. Falaremos mais sobre a transformada de Fourier e a Análise de Fourier nos próximos posts.
Para terminar, falemos de uma das propriedades mais bacanas que certos espaços de Hilbert possuem:
Definição: Dado X um espaço métrico, dizemos que este é separável se existe um conjunto enumerável 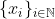 que é denso neste, i.e., para cada x em X, e cada a > 0, existe um k natural tal que
que é denso neste, i.e., para cada x em X, e cada a > 0, existe um k natural tal que
Teorema 2: Se H é um espaço de Hilbert separável, então este é isometricamente isomorfo a l²(N), i.e., existe uma transformação linear contínua e invertível
tal que
Prova: Tal fato é corolário imediato do Teorema 1, se juntarmos com o fato que todo espaço de Hilbert Separável possui base ortonormal (ver exercícios) 
-Exercícios-
1. Prove que As funções contínuas C[0,1] são densas em L²[0,1] (Dica: Aproxime uma função em L² por combinação linear finita de funções características de intervalos. Aproxime estas últimas por contínuas)
2. Prove que todo espaço de Hilbert Separável possui uma base ortonormal (Dica: relacione separabilidade a espaços vetoriais de dimensão finita)
3. Prove o Lema de Grothendieck: Seja M espaço de medida com med(M) finita. Se um espaço E é subespaço fechado de 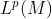 , para algum p maior ou igual a 1 (e não infinito), e só contém funções limitadas, então dim E é finita (Dica: Mostre que, sob essas hipóteses, então a norma p restrita a E é equivalente tanto à norma infinito quanto à norma 2. Utilize este último fato, tomando uma sequência ortonormal em E, e provando que esta possui no máximo uma quantidade fixa de elementos, que seria um absurdo se E tivesse dimensão infinita. Para mais detalhes, veja [1], Exercício 5.29)
, para algum p maior ou igual a 1 (e não infinito), e só contém funções limitadas, então dim E é finita (Dica: Mostre que, sob essas hipóteses, então a norma p restrita a E é equivalente tanto à norma infinito quanto à norma 2. Utilize este último fato, tomando uma sequência ortonormal em E, e provando que esta possui no máximo uma quantidade fixa de elementos, que seria um absurdo se E tivesse dimensão infinita. Para mais detalhes, veja [1], Exercício 5.29)
-Referências-
[1] - H. Brezis. Functional Analysis, Sobolev Spaces and Partial Differential Equations.Springer, 2011.
Comentários
Postar um comentário
Você pode comentar! A equipe do blog encoraja todos a comentar.
Porém, lembre-se que comentários que desrespeitem as regras abaixo serão excluídos:
-É proibido ofender qualquer pessoa ou grupo em seu comentário.
-Os comentários deverão ser minimamente relacionados com o tópico. Lembrem-se, estamos falando de um blog de matemática!
-Proibido flood.
-Proibido palavras de baixo calão.
-Proibido colocar qualquer tipo de conteúdo improprio para menores de 18 anos (há menores de idade que acessam o blog).
A equipe do blog agradece seu comentário, e tenha certeza que será muito enriquecedor. Tentaremos respondê-los o quanto antes possível.